“Development of a Python program for investigation of reaction-diffusion coupling in oscillating reactions”
Github
Introduction
The Brusselator is a model developed by I. Prigogine and R. Lefever at the Universite Libre de Bruxelles in Belgium. [16] developed for the description of nonlinear systems. The model includes some assumptions [12, 11], such as irreversible reactions (![]() for
for ![]() and constant reactant and product species concentrations A, B, C and D. Realistically, this happens by constant addition of A and B and removal of C and D.
and constant reactant and product species concentrations A, B, C and D. Realistically, this happens by constant addition of A and B and removal of C and D.
![]()
![]()
![]()
![]()
![]()
![]()
With the assumptions of chapter 2.1, the dierential kinetic time laws of the species X and Y can be derived. The concentration of a species is noted with square brackets. The concentration notation is assumed to be dimensionless in the following, since there is a mathematical consideration of the issue. With ![]() and
and ![]() for
for ![]() the differential time laws follow.
the differential time laws follow.
![]()
![]()
Spatially Homogeneous Brusselator
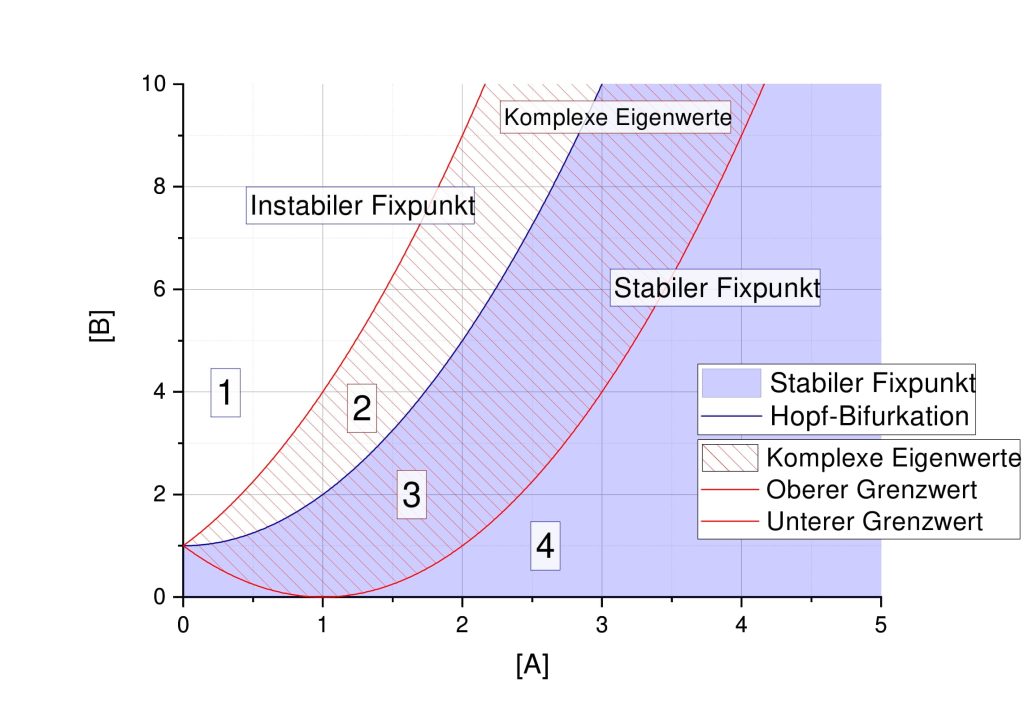
Dynamic Analysis of the Spatially Homogeneous Brusselator
This part is rather long and thus shortened. The full version is shown in detail in my thesis. The fixpoint can be calculated. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\renewcommand{\arraystretch}{2} \begin{bmatrix} \dfrac{\text{d} U}{\text{d} t} \\ \dfrac{\text{d} V}{\text{d} t} \end{bmatrix} = \begin{bmatrix} \dfrac{\delta f}{\delta \left[X\right]} \dfrac{\delta f}{\delta \left[Y\right]} \\ \dfrac{\delta g}{\delta \left[X\right]} \dfrac{\delta g}{\delta \left[Y\right]} \end{bmatrix} \begin{bmatrix} U \\ V \end{bmatrix}= J_{g,f}\left(\left[X\right],\left[Y\right] \right) \begin{bmatrix} U \\ V \end{bmatrix} = \begin{bmatrix} - k_2 \left[B\right] + 2 k_3 \left[X\right]\left[Y\right] - k_4 & k_3 \left[X\right]^2 \\ k_2 \left[B\right] - 2 k_3 \left[X\right]\left[Y\right] & - k_3 \left[X\right]^2 \end{bmatrix}\begin{bmatrix} U \\ V \end{bmatrix}\]](https://lukaswittmann.com/wp-content/ql-cache/quicklatex.com-45a2216b13773039447b14bca6aed1c7_l3.png)
![Rendered by QuickLaTeX.com \[\lambda_{1,2}=\left[ \begin {array}{c} {\dfrac {-{[A]}^{2}+[B]-1}{2}}+{\dfrac {1}{2}\sqrt {{[A]}^{4}-2\,{[A]}^{2}[B]-2\,{[A]}^{2}+{[B]}^{2}-2\,[B]+1}}\\ \dfrac {-{[A]}^{2}+[B]-1}{2}+{\dfrac {1}{2}\sqrt {{[A]}^{4}-2\,{[A]}^{2}[B]-2\,{[A]}^{2}+{[B]}^{2}-2\,[B]+1}}\end {array} \right]= \dfrac{\tau \pm \sqrt{\tau^2-4 \Delta}}{2}\]](https://lukaswittmann.com/wp-content/ql-cache/quicklatex.com-423de9771a762e6be1163d95155f5a9f_l3.png)
Limit Cycle
With the use of Poincaré–Bendixson theorem, it can be shown, that a limit cycle is possibile. This depends on the domain present. The proof for the Brusselator model is carried out in [25, p. 42] or more generally in [26, p. 196].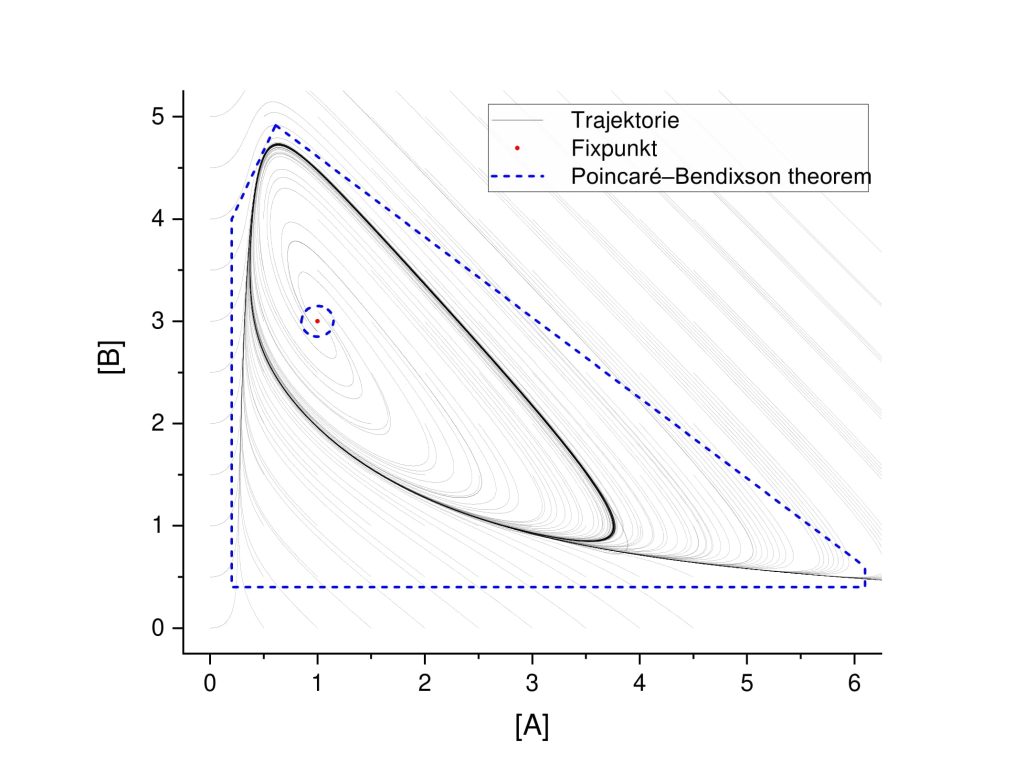
Reaction-Diffusion System of Brusselator
Both differential equations can now be advanced by using the second Fick’s law. ![]()
![]()
Dynamic Analysis of the Reaction-Diffusion System
It is found, that the Fixpoint equals the one of the spartially homogenous system. ![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \renewcommand{\arraystretch}{1.2}[C]=\begin{bmatrix} [X] \\ [Y] \end{bmatrix}](https://lukaswittmann.com/wp-content/ql-cache/quicklatex.com-c2bba7992cd84d9796b8b5d1b37ba1c3_l3.png) ,
, ![Rendered by QuickLaTeX.com $\renewcommand{\arraystretch}{1.2}k\left([C]^*+\sin(\omega r + \phi)\Delta[C]\right)=\begin{bmatrix}f\left([X]^*+S\Delta[X],[Y]^*+S\Delta[Y]\right) \\ g\left([X]^*+S\Delta[X],[Y]^*+S\Delta[Y]\right) \end{bmatrix}](https://lukaswittmann.com/wp-content/ql-cache/quicklatex.com-cbdc1db88ee8d451d3ddd17bd1b137a4_l3.png) and
and ![]()
![Rendered by QuickLaTeX.com \[\renewcommand{\arraystretch}{2}k\left([C]^*+\sin(\omega r + \phi)\Delta[C]\right) \approx k\left([C]^*\right)+\begin{bmatrix}\dfrac{\delta f([X],[Y])}{\delta [X]} & \dfrac{\delta f([X],[Y])}{\delta [Y]}\\\dfrac{\delta g([X],[Y])}{\delta [X]} & \dfrac{\delta g([X],[Y])}{\delta [Y]} \end{bmatrix}\sin(\omega r + \phi)\Delta[C]\]](https://lukaswittmann.com/wp-content/ql-cache/quicklatex.com-35242ca5b9aa262d85dfacb864a6e5ae_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[J_{g,f}\left(\left[X\right],\left[Y\right] \right)-D\omega^2 =\renewcommand{\arraystretch}{2}\begin{bmatrix}\dfrac{\delta f([X],[Y])}{\delta [X]} & \dfrac{\delta f([X],[Y])}{\delta [Y]}\\\dfrac{\delta g([X],[Y])}{\delta [X]} & \dfrac{\delta g([X],[Y])}{\delta [Y]}\end{bmatrix} - \begin{bmatrix} D_x\omega^2 & 0 \\ 0 & D_y\omega^2 \end{bmatrix} \text{.}\]](https://lukaswittmann.com/wp-content/ql-cache/quicklatex.com-b2f28221377340e0553a1e5e7db21708_l3.png)
![Rendered by QuickLaTeX.com \[D_{y}^{grenz,1}\left([A],[B],D_x \right) = \dfrac{\left([B]+1\pm 2\sqrt{[B]}\right)[A]^2D_x}{[B]^2-2[B]+1}\]](https://lukaswittmann.com/wp-content/ql-cache/quicklatex.com-d8179b6ddff4689127101926607b6f0a_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[[B]_T\left([A],D_x,D_y \right) = \left(1+[A]\sqrt{\dfrac{D_x}{D_y}}\right)^2]\]](https://lukaswittmann.com/wp-content/ql-cache/quicklatex.com-923f74acff77d20629d8f295991b42b4_l3.png)

![Rendered by QuickLaTeX.com [A] = 1](https://lukaswittmann.com/wp-content/ql-cache/quicklatex.com-4e892a87cb1b7281d84049fc1e1f05a6_l3.png) und
und ![Rendered by QuickLaTeX.com [B]=3](https://lukaswittmann.com/wp-content/ql-cache/quicklatex.com-93282da6e67f258cdef855bbb5da3031_l3.png) , welche stabile Fixpunkte und instabile Fixpunkte liefern sowie die Turing-Stabilität
, welche stabile Fixpunkte und instabile Fixpunkte liefern sowie die Turing-Stabilität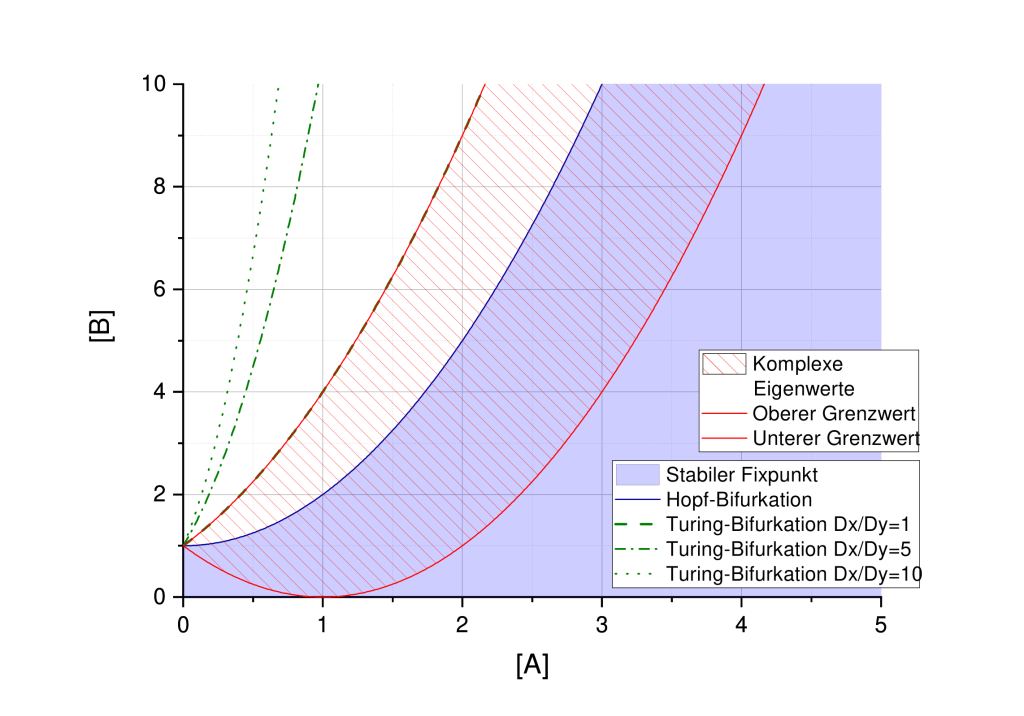
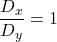 ,
, 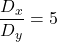 , and
, and 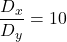 , which provide stable fixed points and unstable fixed points, and Turing stability.
, which provide stable fixed points and unstable fixed points, and Turing stability.
Leave a Reply