Simple Python program for calculation and visualization of 2d and 3d reciprocal space
(unit cell of the famous Si(111) 7×7 reconstruction)

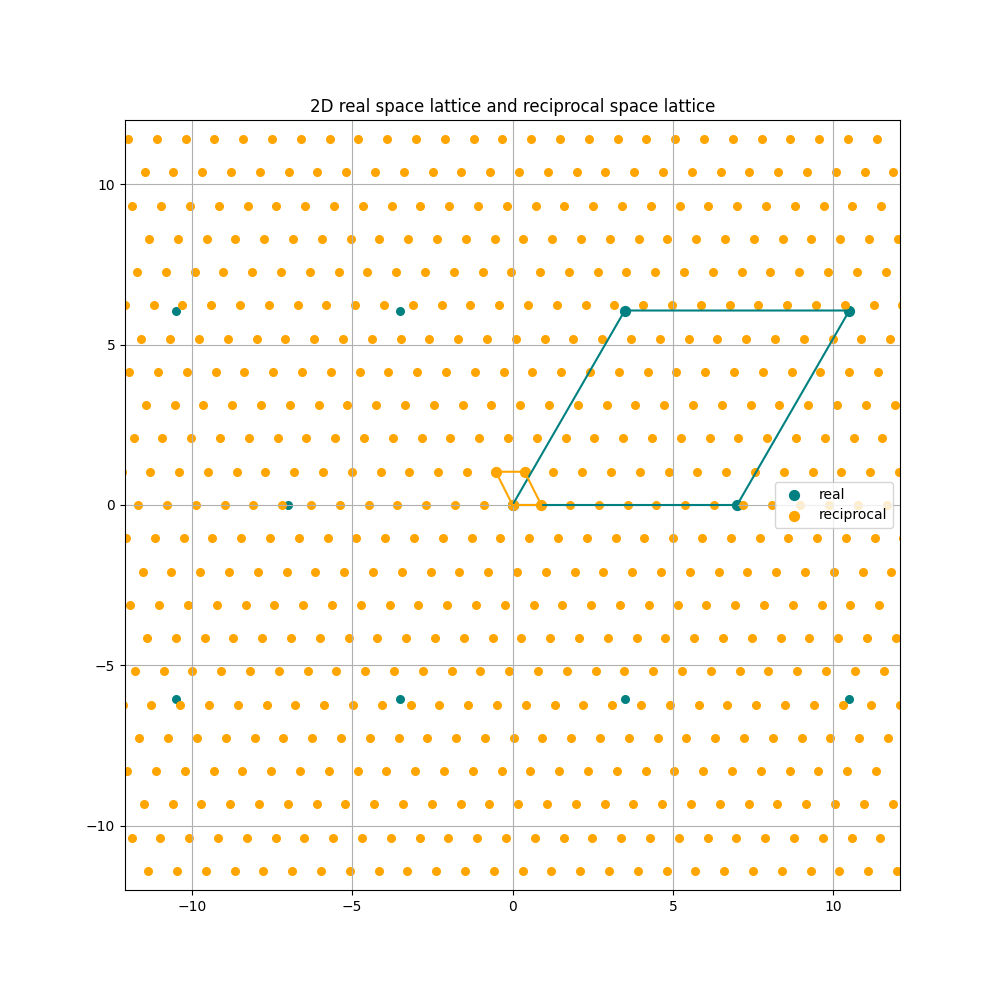
(triclinic real space Bravais lattice)
Motivation
While working with spectroscopic methods to determine surface properties in the field of ultrafast electron dynamics, I wanted a tool to calculate and visualize real and reciprocal space unit cells and lattices in two and three dimensions.
Github
Theory
Calculation of reciprocal lattices is straight forward and only requires small amount of formulas. These can be found anywhere and are even well explained on Wikipedia.
2D reciprocal space
With the condition for the reciprocal basis
![]()
where ![]() is the primitive vector matrix for real space and
is the primitive vector matrix for real space and ![]() for reciprocal space and
for reciprocal space and ![]() is the Kronecker delta. With this is easy to multiply with the explicit matrix inverse to get
is the Kronecker delta. With this is easy to multiply with the explicit matrix inverse to get
![]()
This can now be used to calculate the 2d reciprocal unit vectors.
3D reciprocal space
For the calculation in 3d is as straight forward. By using the scalar triple product, the volume of the unit cell can be calculated.
![]()
The primitive reciprocal vectors can be calculated.
![]()
![]()
![]()

Leave a Reply