Schrodinger Equation Potential Well Solver

Introduction

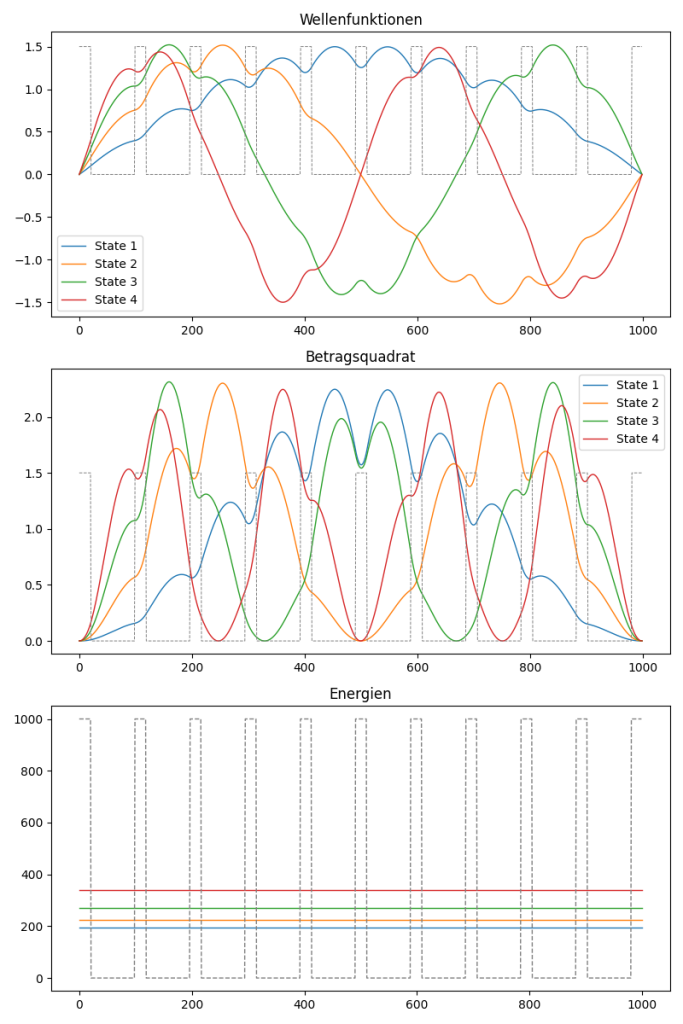
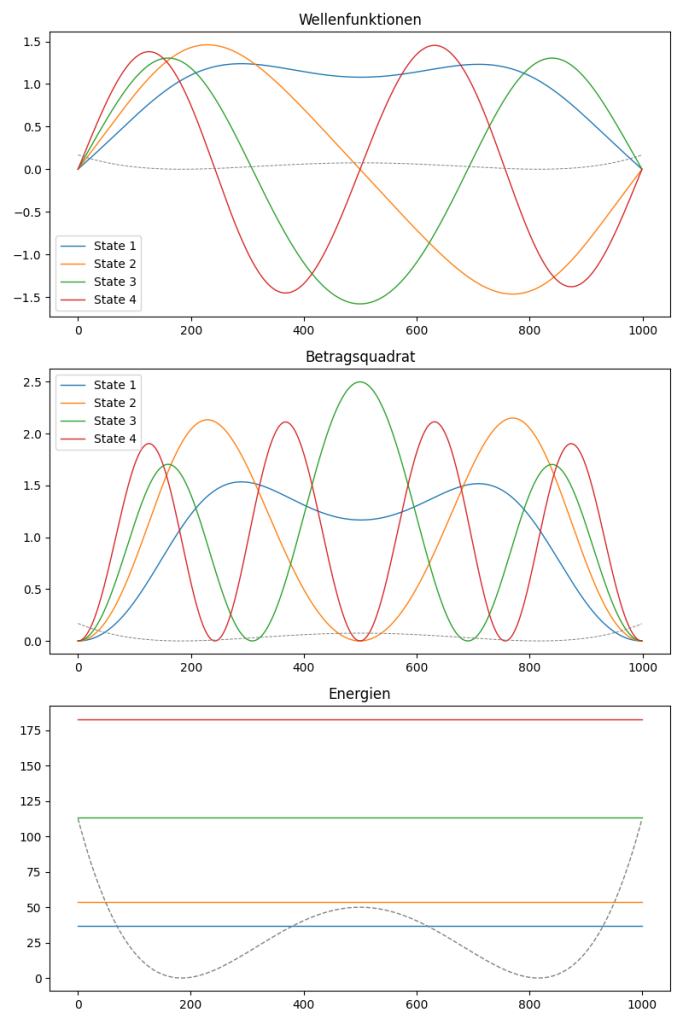
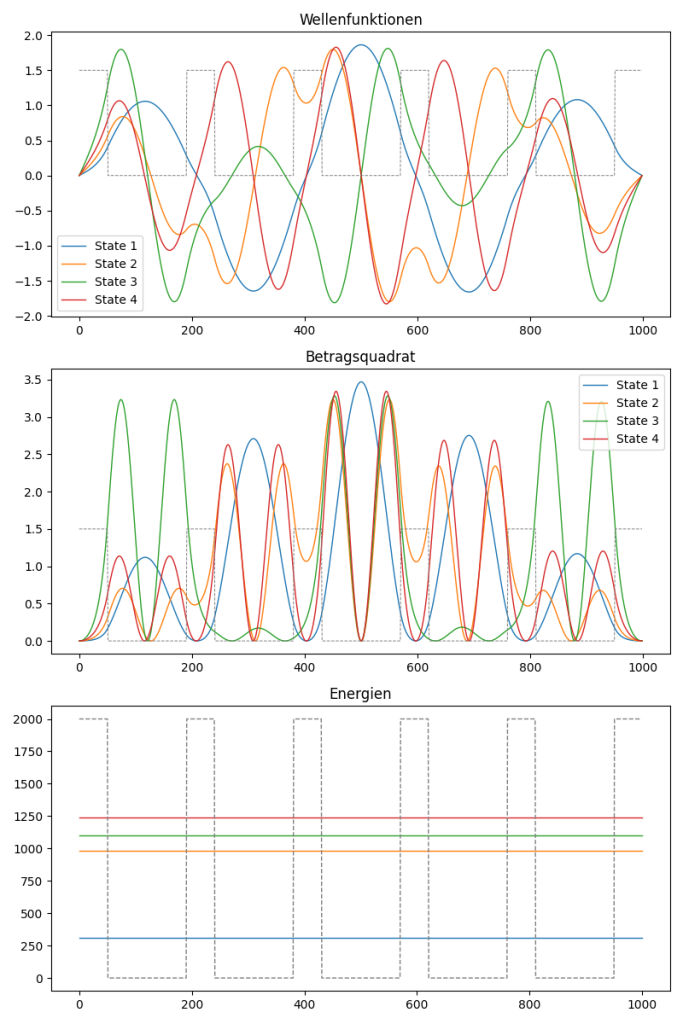
The goal was to be able to solve the one dimensional Schrodinger’s equation of a particle in a box with a custom potential. This was done by a numeric approach using the Verlet algorithm below.

$\psi(x_i)=2\psi(x_{i-1})-\psi(x_{i-2})+\psi''(x_{i-1})\Delta x^2$

$\psi''(i) = \psi(i)(V(i) - E)$

Followed by normalization.

$\sum_{i=1}^{i=max} \psi(x_i)^2 \Delta x = C^2$

$\psi_{norm} (x_i)=\dfrac{1}{C} \psi (x_i)$

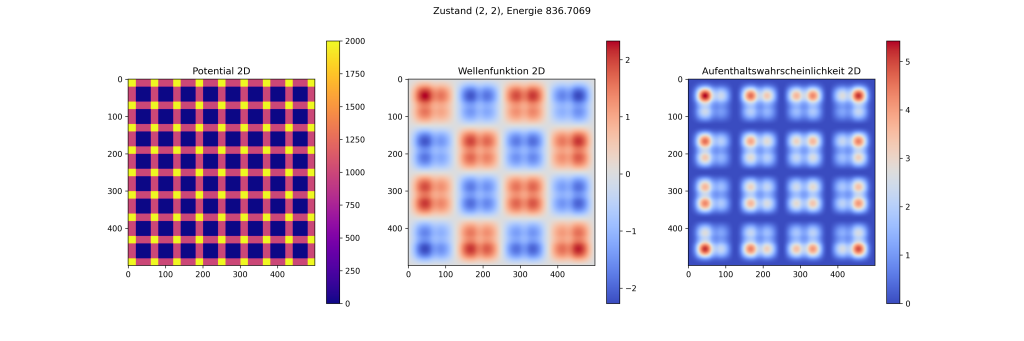
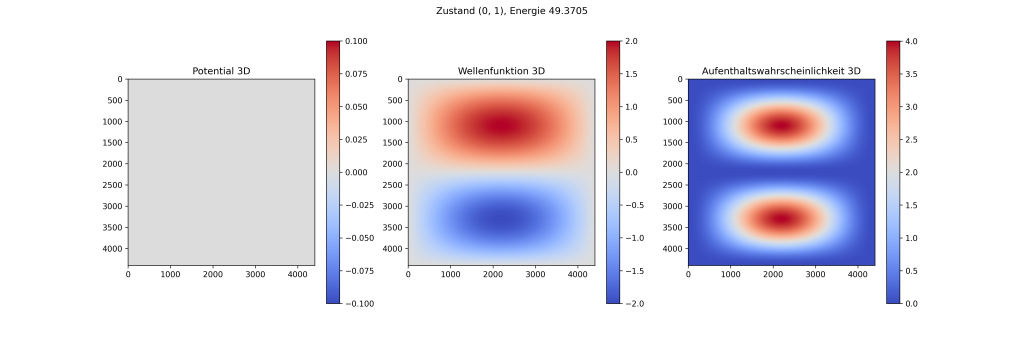
This one dimensional solution can easily be extended to be multidimensional. For two dimension this works as follows.

$V(x,y)=V(x)+V(y)$

$\Psi(x,y)=\psi(x)\psi(y)$

This project was originally implemented using Maple in the optional course “theoretical Chemisty” in my Bachelor’s.

Github

The goal was to be able to solve the one dimensional Schrodinger’s equation of a particle in a box with a custom potential. This was done by a numeric approach using the Verlet algorithm. The one dimensional solution was then extended to two dimensions.
https://github.com/lukaswittmann/schrodinger-equation-potential-well
0 forks.
1 stars.
0 open issues.

Recent commits:

Lukas Wittmann

Schrodinger Equation Potential Well Solver

Introduction

Github

Leave a Reply Cancel reply