Development of a Python program for investigation of epidemic developement
Introduction
With the idea of wanting insight into the pandemic with the possibility of vaccination breakthroughs, I developed an advanced version of the SRIVD-model. For this, the following iterative algorithm was created:
(1) ![\begin{gather*}S[i] = S[i-1] + (- ((\beta[i-1] * I[i-1] * S[i-1]) / (N)) + \sigma[i-1] * R[i-1] - \alpha[i-1] * S[i-1]) * dt\\I[i] = I[i-1] + (((\beta[i-1] * I[i-1] * S[i-1]) / (N)) - \gamma[i-1] * I[i-1] - \delta[i-1] * I[i-1]) * dt\\R[i] = R[i-1] + (\gamma[i-1] * I[i-1] - \sigma[i-1] * R[i-1]) * dt\\V[i] = V[i-1] + (\alpha[i-1] * S[i-1]) * dt\\D[i] = D[i-1] + (\delta[i-1] * I[i-1]) * dt \end{gather*}](https://lukaswittmann.com/wp-content/ql-cache/quicklatex.com-7b3e9947355229b63a71a06e9ff682bc_l3.png "Rendered by QuickLaTeX.com")
For this, the following variables were used:
- Rate of infection
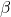
- Recovery rate
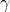
- Death rate
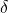
- Vaccination rate
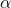
- Susceptibility rate (recovered to susceptible)
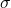
- Rate of infection for vaccinated
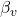
- Recovery rate for vaccinated
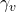
- Death rate for vaccinated
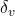
- Susceptibility rate – vaccinated to susceptible
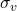
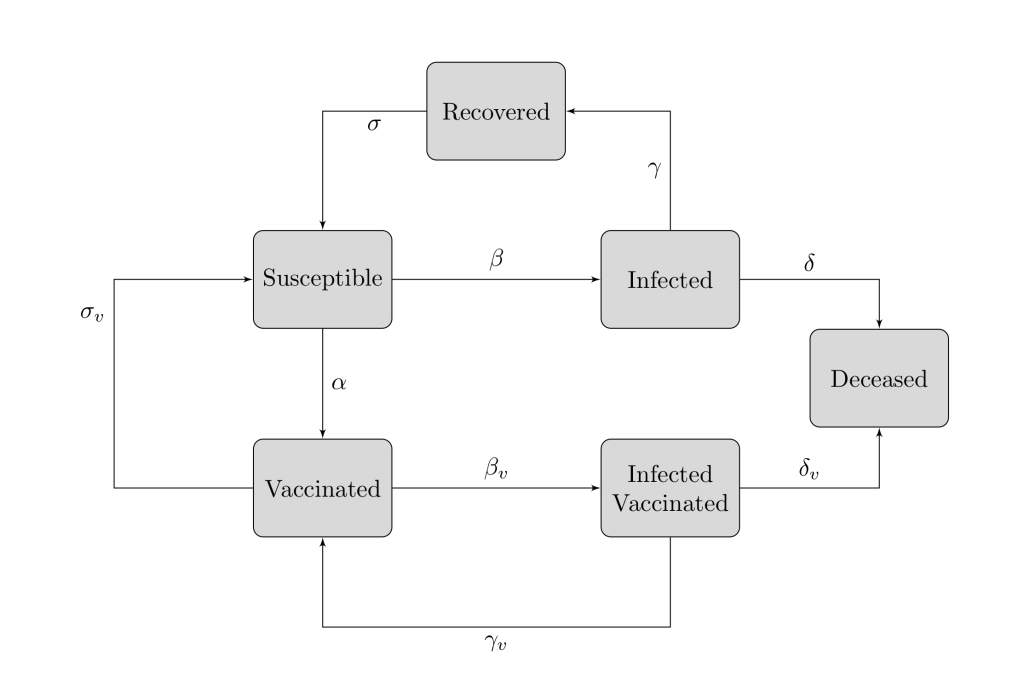
Below, there is a scheme which describes the above equations and my idea.
Github
Simulations
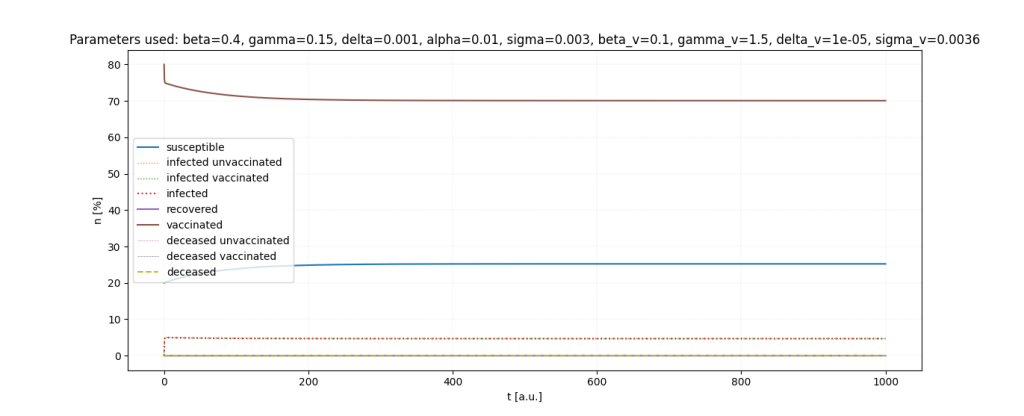
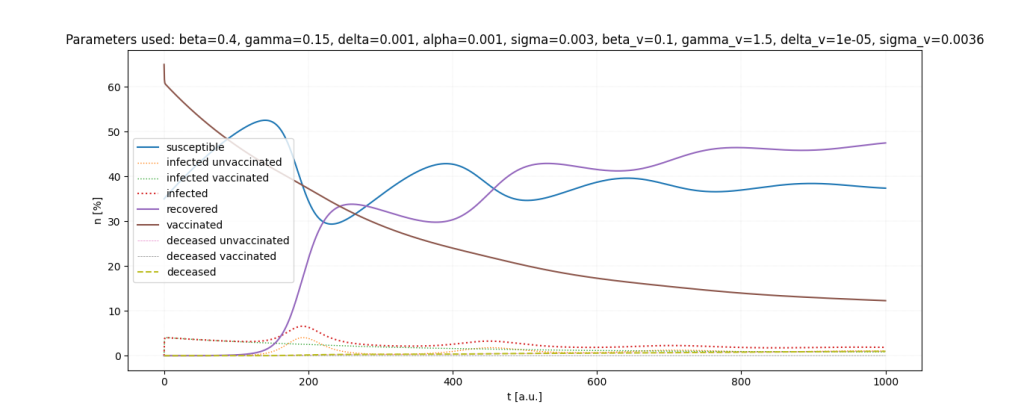
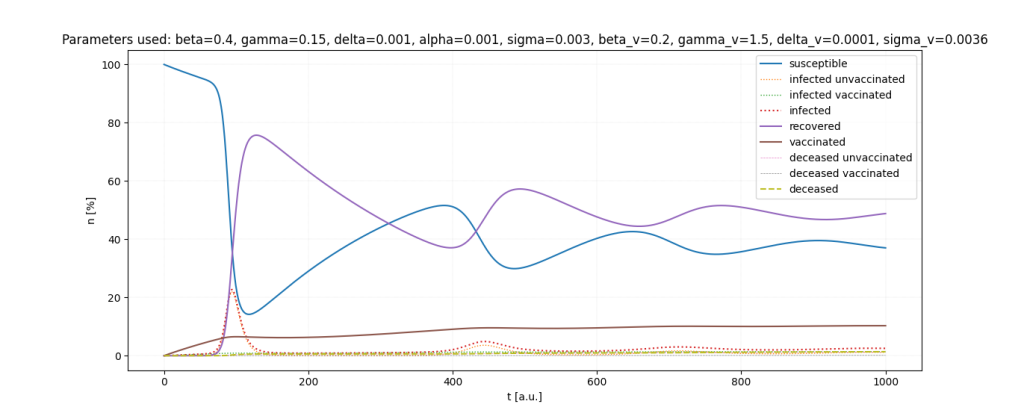
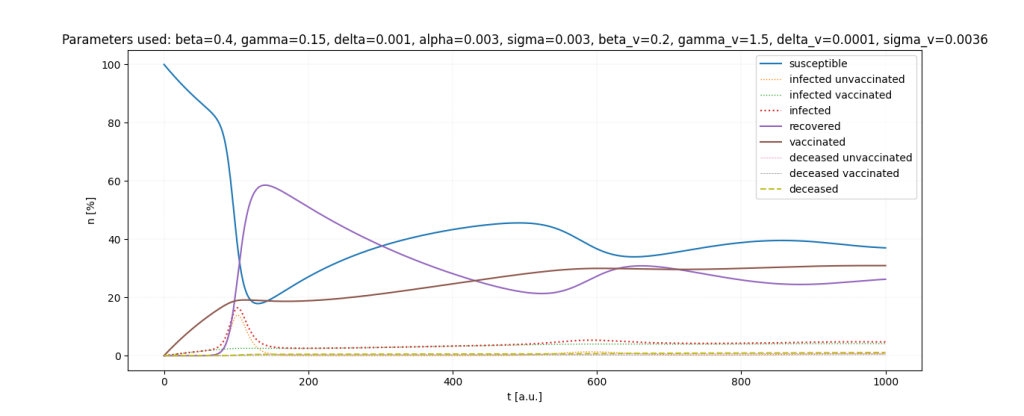
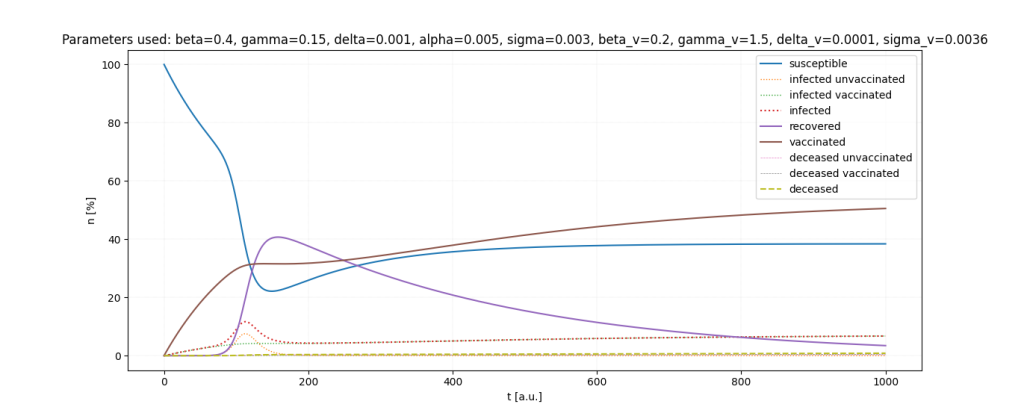
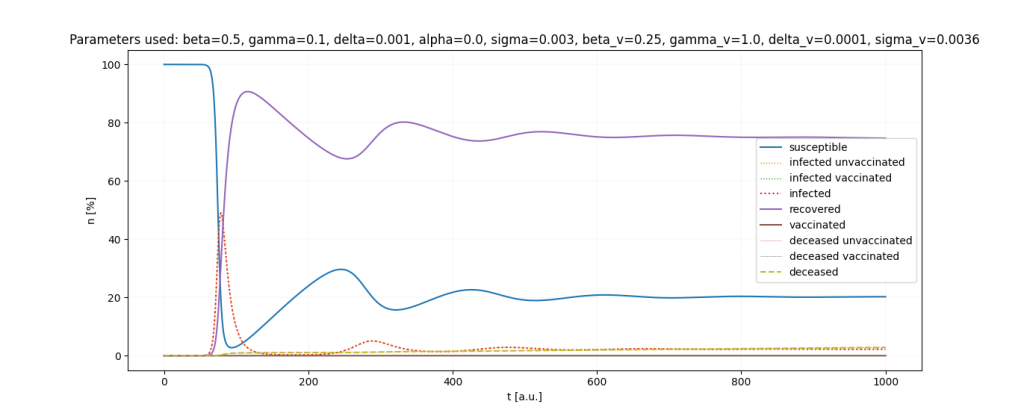
It is a lot of fun to just play around with the parameters.
Important: All parameters and ratios I used are made up. I used those, because they seemed somewhat realistic in certain scenarios and show interesting behaviour in the simulations.
Leave a Reply